Human brain theory

This chapter, created on 20 January 2025, has been significantly changed and expanded. This is because I constantly review all theoretical elements of my brain theory and, in particular, compare the consistency of my theoretical neural circuits with the cytoarchitecture of the vertebrate brain, thereby resolving any contradictions. In my mind, I go through each of the circuits I describe thousands of times and mentally check whether the analytical behaviour can be derived from the circuit architecture. As a result, I have noticed inconsistencies in this chapter that needed to be corrected. A comparison with theoretical elements of artificial neural networks and the theory of AI itself also required changes. Some insights only became comprehensible in the context of AI theory.

If a reader notices that elements of my brain theory contradict each other or are not entirely compatible when comparing older and more recent texts, they can always assume that the more recent texts are closer to the truth than the older ones. For example, in my very first monograph, "Theory of the Neural Circuitry of the Brain and Analytical Thinking," I put forward the hypothesis that the brain works in principle in a binary manner. Terms such as single signal, single signal core, negation, double and quadruple negation of signals appear frequently there. One reason for this is the manipulative nature of many publications at the time, whose authors seemed enthusiastic about the idea that the brain was a kind of computer. Computers at that time, and even today, worked predominantly in binary mode. If a reader were to read the monograph today, they should generally replace the term "negation" with "inversion". The algorithm classified as negation at the time is in fact signal inversion. Taking this correction into account, the monograph is essentially correct and still relevant today. In my defence, I can say that in this monograph, I described not only negation nuclei but also inversion nuclei, in which the inhibition is not total but only relative. And I pointed out even then that it could be extremely difficult to distinguish negation nuclei from inversion nuclei because the cytoarchitectonic circuitry is almost identical.

This correction concerns essential nuclei: the basal ganglia nuclei and the cerebellar nuclei are not negation nuclei, but inversion nuclei.

I reserve the right to make further corrections to the existing monographs. With increasing knowledge, it is much easier to identify errors in theory than during the hypothesis formation stage. But now let us move on to Chapter 20.

 

Many brain researchers are convinced that the pontocerebellum is a kind of natural neural network. It could also be assumed that it is a deeply layered neural network. These assumptions are certainly accurate.

But before we prove that the pontocerebellum is a deep neural network, let us trace the path that the cerebellum has taken in the course of evolution. We are particularly interested in how the early spinocerebellum developed into the later pontocerebellum. Just as the primitive vestibulocerebellum gave rise to the spinocerebellum when motor signals were equated with vestibular signals and, through their integration, part of the vestibulocerebellum became the spinocerebellum, part of the spinocerebellum developed into the pontocerebellum. Simply put, an additional, different input was processed. The neural circuitry remained essentially the same.

This is the special feature of the cerebellum, that it has the same, recurring neural circuit in all its subsystems. This is why its mode of operation is so difficult to understand and can only be understood in the context of the neural circuit of its input suppliers and output receivers. This in turn requires extensive neurological knowledge.

I have described the development of the vestibulocerebellum in detail in my monograph "Brain Theory of Vertebrates" in chapter 4.9 "The Transformation of the Vestibular Sense and the Development of the Cerebellum". Of course, the explanations provided there are to be understood as a theory, i.e. as a hypothesis, even though there is very strong evidence that this was indeed the case at the time. Nevertheless, allow me to summarise the explanations provided there again here in brief.

The vestibular sense underwent structural changes in the course of evolution. In this monograph, we refer to its earliest form as the " " or "paleovestibular sense" ( ). This can be found, for example, in polyps.

In a vestibular cavity, a fluid-filled cavity, a grain of sand that had entered through a small opening rolled back and forth. Due to gravity, it was located at the lowest point of this vestibular cavity. This was lined with hair cells, which were bent by the weight of the grain of sand and thus stimulated neuronally. When the animal deviated from the desired standard position, other hair cells were stimulated, whose e action potentials led to muscle contraction. These corrective movements resulted in the standard position being resumed.

The paleovestibular sense was not the best solution in terms of mechanics and design.

A disadvantage of this vestibular sense was its dependence on the random presence of a grain of sand in the vestibular cavity. The movements of the grain of sand also caused the hair cells to wear out. These disadvantages led to an evolutionary redesign of the vestibular sense.

A gelatinous protective layer formed, embedding the hair cells to protect them and extend their lifespan. The rolling grain of sand was replaced by small, fixed crystalline secretions (statoconia) on the gelatinous mass, which were formed by the organism itself. This is how the neovestibular sense developed.

The self-generated statoconia were now distributed fairly evenly across the gelatinous mass. Their own weight exerted pressure on the nearby hair cells. However, the hair cells located at the deepest point of the vestibular cavity were only slightly bent and were therefore the least stimulated. The hair cells were now comparable to leaf springs clamped on one side with a small weight at the free end. While in the paleovestibular sense the activated hair cells at the lowest point of the vestibular cavity were maximally stimulated, in the neovestibular sense these hair cells were not stimulated at all. The hair cell located at the lowest point was aligned exactly parallel to the direction of gravity and was therefore the least bent; its firing rate was almost zero, i.e. extremely minimal. However, maximum excitation was required at precisely this point.

Nature knew how to help itself: it invented signal inversion.

Signal inversion requires a stronger mean signal, which was available at every level of the segmented nervous system because there were mean centres there. In the vestibular segment, this mean signal was linked to every vestibular signal. The mean signal was distributed across as many inversion neurons as there were hair cell signals. Each hair cell signal now inhibits its associated inversion neuron , which was excited by the mean centre.

This reversed the signal strength. If the hair cell signal was zero, the mean signal remained in the inversion neuron as a residual signal. If the hair cell signal was of medium strength, it inhibited the mean by only half, and the output of the inversion neuron was also of medium strength. A very strong hair cell signal ( ) inhibits the signal mean value so strongly that the output signal of the inversion neuron became zero.

The inhibition of the mean signals in the inversion neurons provided an inverted vestibular signal, which now again took on the strongest value at the lowest point of the vestibular cavity. Since the inversion neurons used excitatory neurotransmitters, the output was excitatory and could be used for motor position correction.

But how did the hair cell signals manage to inhibit a mean signal of the vestibular level in the first place?

Here, contralateral inhibition proved useful in the early stages of evolution. All signals could reach the contralateral side of the body via the side-switching nucleus of their level (their segment) and exert an inhibitory effect there. This is how contralateral inhibition was realised in the early stages of evolution. Both halves of the body were in neural competition with each other.

The output of the hair cells of the vestibular system could also pass to the opposite side via the side-switching nucleus, where it was switched to inhibitory transmitters. This is how contralateral inhibition was initially organised. However, a change was on the horizon. These inhibitory signals were able to find their way to the mean value nucleus of the vestibular system and generate their own output neurons (inversion neurons), which in turn continued to receive mean value excitation. The inhibition of the mean excitation led to signal strength reversal, i.e. signal inversion. The output signals of the neovestibular sense were then usable again for motor control because they were maximum-coded. In later stages of evolution, many signals, including inhibitory signals, were incorporated into the mean value formation of the existing mean value nuclei.

The side-changing nucleus, through which the vestibular signals moved to the opposite side, developed into the olivary nucleus. The switching neurons, which switched the vestibular signals from the excitatory transmitter to the inhibitory transmitter GABA, are now called Purkinje cells. The inversion neurons formed the nucleus fastegii.

The Purkinje nucleus formed the vestibulocerebellum together with the nucleus fastegii. It served to invert the vestibular signals of the neovestibular sense. These were transferred from the minimum-coded state to the maximum-coded state, thereby becoming usable for motor functions.

In the course of evolution, other signals also found their way into the vestibulocerebellum, primarily signals from the motor system ascending from the trunk and from the developing sense of touch and pain. Since the spinal cord is referred to as the medulla spinalis, these are spinal signals that are associated with the spinal cord. In the course of evolution, they found their way into the vestibulocerebellum.

The part of the vestibulocerebellum that received these motor signals soon formed a separate part of the cerebellum, which is called the spinocerebellum because it receives spinal signals. It inverts the motor signals of the contralateral half of the body and excites the motor antagonists with the inverted signals. In this way, the excitation of a muscle on one side of the body was converted into an inverse excitation for the antagonist muscle. Neurologists also refer to this inverse motor excitation as co-activation. As a result, both muscles are tense and form a joint angle whose value depends on the tension ratio between the two partners.

This coactivation ensured better body tension and was an important prerequisite for the transition of aquatic animals to land. In this way, the influence of gravity could be compensated for.

It should be noted that the spinal signals reached the spinocerebellum via the olivary nucleus, creating a climbing fibre projection into the spinocerebellum. Both the vestibular and spinocerebellum can only perform the task of signal inversion because the signals reached the Purkinje cells via the climbing fibre system, whose inhibitory output in the pre-excited cerebellar nuclei led to signal inversion. Much later, during an expansion phase of the cerebellum, a mossy fibre projection to the spinocerebellum also developed, but signal inversion remained its main task. 

Contrary to earlier views, I would like to understand signal inversion algebraically as the inverse operation of addition. I initially assumed the equally possible interpretation as the inverse operation of multiplication because it was widely reported that neurons generally work non-linearly. However, I no longer support this view in general.

When interpreting signal inversion as an inverse operation to addition, a firing rate f with a mean firing rate f_mwould be combined with an inverse firing rate f^*according to the formula

.

The firing rate of mean neurons with a sufficient number of input sources and sufficiently strong excitation leaves the linear range and asymptotically approaches the maximum firing rate f_max. This maximum firing rate is caused by the refractory period. This is the time a neuron needs after firing an action potential to generate a new action potential. This limits the firing rate upwards. In this case, which is likely to apply especially in later evolutionary stages of " ", the formula

,

where f_m  represents the average firing rate, which corresponds to approximately half of the maximum firing rate.

Signal inversion can be achieved in the vertebrate brain in two different ways:

-         Signal inversion with external mean signal

-         Signal inversion with internal averaging.

The vestibulocerebellum and the spinocerebellum work with an external mean signal, which they obtain from the reticular formation. Only the pontocerebellum changes this by switching to internal averaging.

The development of the spinocerebellum is also described in detail in the aforementioned monograph. Particular attention was paid to the interactions between motor and sensory signals.

However, we should now analyse how it works and focus on the processing of motor signals. Parallel to the formation of the spinocerebellum, the double layers in the cortex began to develop, emerging from the uppermost layer of the early ladder-like nervous system.

In the previous chapter, we showed that a double-layer structure of the nucleus olivaris can be derived from the double-layer structure of the cortex. Let us consider the ipsilateral half of the cortex as an example.

The lower double layer in the ipsilateral cortex is the more evolutionarily ancient one. It has the body side marker of the contralateral side, because the signals must pass through a signal crossing in a descending and ascending direction, the necessity of which results from the structure of the vestibular sense. This is how they reach the opposite side, where the contralateral body side marker predominates.

The upper ipsilateral double layer is assigned to the ipsilateral side of the body, because the ascending signals from the ipsilateral side passed via the lateral nucleus (nucleus olivaris) to the contralateral side and from there to the cerebellum. The contralateral cerebellum projects back to the cortex, where the signals change sides again and reach the ipsilateral side. Thus, the cortical double layer receives an on signal from one half of the body and an off signal from the contralateral half of the body. The latter off signal is generated by signal inversion in the cerebellum from the on signal.

Since each half of the body has its own body side marker, which is passed on via the projection axons in the system, the contralateral body markers arrive in the lower layer of the double layer and the ipsilateral body markers in the upper layer.

This means that the on-off markers are already present in the cortical double layer of input neurons, which are later transmitted via projection to the olivary nucleus and the cerebellum, leading to the recognised stripe-like distribution in the cerebellar cortex. I described this in detail in the monograph "Gehirntheorie des Menschen" (Brain Theory of Humans) in Chapter 17, "Die Doppelschichtentheorie nach Andreas Malczan" (The Double Layer Theory According to Andreas Malczan).

During the further evolution of vertebrates, signal divergence developed. Important signals were distributed to several output neurons for transmission, with signal transmission occurring in parallel on their axons. This improved data security. Individual neurons could die without jeopardising the functioning of the organism.

Signal divergence occurred in the nuclei, which were evolutionarily younger neoplasms. These were the substructures belonging to the cerebellum, as this neoplasm was only recently developed.

We assume that signal divergence originated in the olivary nucleus. This was the motor side-switching nucleus of the primitive brain of vertebrates. The following figure symbolically illustrates the gradual emergence of signal divergence. M(_{1) ,}M(_{2) ,}M(₃₎ and M(₄₎ denote the muscle signals of a (simple) joint.

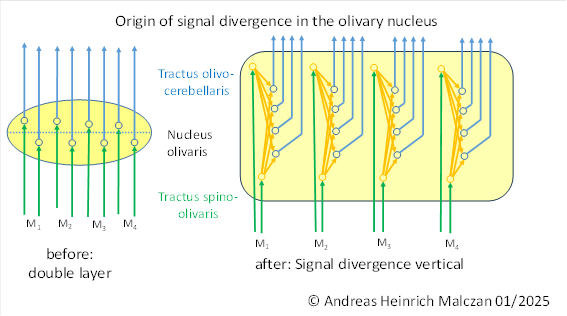
Before signal divergence, the olivary nucleus consisted of a double layer of output neurons. One layer conducted the on signals of the flexor muscles to the cerebellum, while the second layer was responsible for the off signals. The arrangement of the two types of neurons in different layers was a consequence of the principle of spatially separating different modalities. This separation of modalities is (apparently) controlled by marker substances that are responsible for topological order.

In contrast to earlier views (see brain theory of vertebrates), I assume that the signal divergence in the olivary nucleus occurred perpendicular to the surface of this neuron core. The reason for this was the assumption that the thickness of the output layer would be easier to achieve than a growth in width, in which case it would be completely unclear how the marker situation would develop. In the cross-section of the olivary nucleus, it can be seen that it is formed by a fairly thick layer of neurons.

If we indicate the on marker with green and the off marker with red in the figure above, the following image emerges.

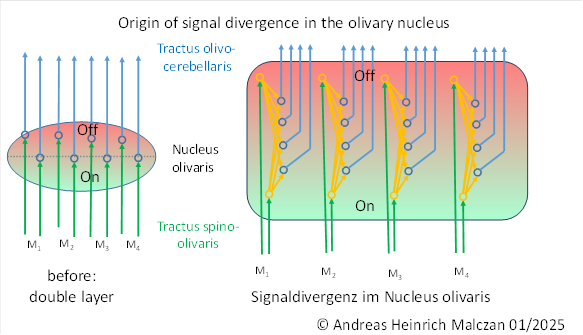
What is special is that not only the output signals are transported via the output axons, but also the marker substances, so that these are passed on to the subsequent structures.

The output signals of the on channel are inverse to the signals of the off channel.

The stronger the on signal of a joint, the weaker the corresponding off signal. The signal strengths were inversely proportional to each other. Only in the middle of the joint were both signal components equally strong.

After signal divergence, each output neuron received two signal components: the on signal and the off signal. Depending on where an output neuron was located in the olivary nucleus, it received different strengths of on and off components from the two associated input neurons. This was due, on the one hand, to the fact that the joint angle usually deviated from the middle position and, on the other hand, to signal attenuation during the propagation of the signal components, which increased exponentially with distance.

As the distance of an output neuron to the on-input neuron increased, the distance to the off-input neuron decreased at the same time, so that less signal strength was received from the input signal of the on-neuron and more signal strength was received from the input signal of the off-neuron. The superposition of both signal components in the output neuron resulted in a strictly convex function with a clearly defined minimum. The position of the minimum is clearly determined by the signal strength ratio of the two input signals, i.e. by the ratio of the signal strength of the on signal to the signal strength of the off signal. To calculate the extreme value, the differential quotient of the superposition function must be set to zero and solved for the signal strength parameters.

We use the following figure to derive the formulas.

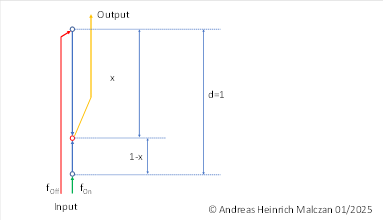
The firing rate f_On  of an on signal reaches the lower input neuron of the nucleus olivaris (axon green). The corresponding off signal with the firing rate f_Off  arrives at the input neuron in the upper layer (axon red). Both input axons are considerably thick, so that there is approximately no signal attenuation. This no longer applies to the interneurons. On the one hand, their axons are quite thin, and on the other hand, they do not have an insulating myelin sheath, since the olivary nucleus belongs to the grey matter. This results in distance-dependent signal attenuation.

A randomly selected output neuron (red) is shown. This receives the excitation of the on signal, which, however, must travel the path 1-x and undergoes signal attenuation because the axons within the nucleus olivaris belong to the grey matter and do not have myelin. From the cable equation for unmarked axons, it can be deduced that the input firing rate f(_On)will be exponentially attenuated with increasing distance 1-x.

The same applies to the input firing rate f_Off, where the distance   x must be taken into account.

Therefore, the output neuron (red) receives the following total excitation:

.

Here, λ is the length constant of the output neuron.

We consider that the firing rate f_Off  arose from signal inversion from the firing rate f_On , for which the inversion cerebellum is responsible.  In principle, the equation f_on +  f_off  = f_max  = 2f_m  applies to both partial signals.

The resulting firing rate f is a strictly convex function, since each partial sum is strictly convex. Therefore, a global minimum exists in the domain.

Here, f_on , f_Off  and λ are to be regarded as constants, so that only the variable x remains.

We determine the global minimum by calculating the first derivative and then setting it to zero.

.

We rearrange the equation.

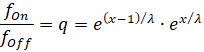
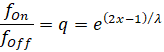
Clearly, for x = ½, the value of q is equal to 1, so that f_on =  f_off  becomes. If both firing rates are identical, the minimum is assumed to be exactly in the middle between the two input neurons. This is because the signal attenuation is identical for both signal components in this special case.

We see that only the quotient of the two firing rates matters.

The global minimum at point x is assumed when the above equation is satisfied. As can be easily seen, x is a strictly monotonically increasing function of q; as q increases, x also increases. The value λ is a constant of the output neuron.

What does this mean for vertebrates and their perception of their own bodies?

When the flexor muscle contracts, f_Onbecomes larger, and the global minimum at point x moves towards larger x values. There is a e output neuron there, which now has the lowest firing rate. If the extensor muscle contracts, the minimum moves towards smaller x values, and the output neuron located there fires the least.

The location where an output neuron fires least encodes the joint angle. Nature has thus found a way to map joint angles to a set of neurons in such a way that the minimum excitation in this set encodes the joint angle.

Now, a neuron that fires minimally at a certain value of a primitive (joint angle) is of little use for motor function, because muscles need strong excitatory signals. Here, the signal inversion of the spinocerebellum proved to be an extraordinary advantage.

The minimum coding is converted back into a more meaningful maximum coding in the cerebellar nucleus by means of signal inversion.

Based on the above explanations, we can summarise as follows:

In the olivary nucleus, signal divergence for motor muscle signals results in minimum coding of joint angles. This is transformed into maximum coding in the cerebellar nucleus.

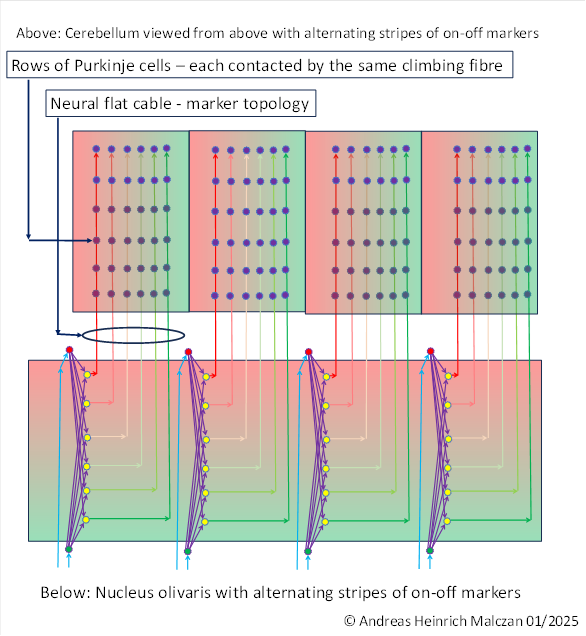
The spinocerebellum projects its excitatory output to the contralateral muscles by activating the output neurons belonging to these muscles in the red nucleus on the same side of the body. The associated fibre tract of the axons involved forms the rubrospinal tract and crosses (for the most part) below the red nucleus to the opposite side, where the contralateral muscles are located. However, in the course of evolution, a cortical projection of the spinocerebellum also forms, so that the cortex, or more precisely the newly formed frontal cortex, also receives the cerebellar output. Here, too, a side change takes place beforehand.

Now we could get philosophical:

The joint angle is encoded in the cerebellum using minimum coding, with the signal minimum representing the joint angle. However, only signal maxima are present in our consciousness. For us, this means that the cerebellum is home to the subconscious. This is generally encoded using minimum coding. Only the signal inversion in the cerebellar nucleus (there are several) transfers the unconscious signal into consciousness by sending it to the cortex. This would make the cortex the material location of consciousness, while the cerebellum represents the subconscious. This hypothesis will be clarified and substantiated later when we identify the pontocerebellum as the seat of the subconscious. But now we can understand how a thought emerges in consciousness ( ). The cerebellum sends it to the cortex.

However, the spinocerebellum was able to significantly improve joint angle analysis. This was aided by the use of marker topology and the evaluation of neighbouring signals.

The double-layer structure of the nucleus olivaris, in conjunction with the onset of signal divergence, gives rise to the striation of the cerebellum with regard to specific marker substances. This striping was experimentally proven in the publication "Purkinje cell neurotransmission patterns cerebellar basket cells into zonal modules defined by distinct pinceau sizes" by Joy Zhou, Amanda M Brown, Elizabeth P Lackey, Marife Arancillo, Tao Lin and Roy V Sillitoe.

We will use the last figure from the previous chapter again to visualise the situation in the cerebellum, with a few minor modifications. The marker concentration for the on marker is marked in green, and that for the off marker in red. The respective marker concentration is transmitted via the axons from the olivary nucleus to the cerebellum.

The upper figure shows how the on-signals from four muscles arrive in the olivary nucleus. Each muscle has an on-signal (green) and an off-signal.

Since the off signal always represents the muscle signal of the motor antagonist, we can also interpret the diagram to mean that the signals from four simple joints arrive in the olivary nucleus. The flexor muscle provides the on signal, while the extensor muscle of the same joint provides the off signal. The two signal strengths are inversely related to each other. Ensuring this was once the original task of the spinocerebellum, which is why we refer to this early part of the spinocerebellum as the inversion cerebellum. It was only with the development of signal divergence in the olivary nucleus that the inversion cerebellum became part of the spinocerebellum.

Signal divergence in the olivary nucleus transmits the signals from each pair of muscles in a joint to the output neurons of a vertical column. In the figure (for example), this consists of 6 output neurons. The axons of these six output neurons form a kind of ribbon, similar to a flat neural cable. The spatial arrangement of the axons in this flat neural cable is caused by the concentration of on-off marker substances, which are transmitted to the cerebellum via the axons, with the marker concentration decreasing with increasing distance.

The olivary nucleus projects into the climbing fibres of the cerebellum. In our case, there are 6 climbing fibres per joint.

The neural flat cable of the climbing fibres transmits the signals to the cerebellum, where (in our example) six chains of Purkinje cells connected in series are contacted. In our example, each chain contains six Purkinje cells that receive the same input from their climbing fibre (view from above!).

In early times, there was only one Purkinje cell per climbing fibre. This was at a time when there was no signal divergence in the olivary nucleus. At that time, the on-signal and the off-signal from the olivary nucleus arrived in the cerebellum and each contacted exactly one Purkinje cell. Thus, there was one on-Purkinje cell and one off-Purkinje cell for each simple joint. Both were located directly next to each other.

As signal divergence in the olivary nucleus increased, not only did the number of output neurons in the olivary nucleus increase, but so did the number of climbing fibres per joint. The number of Purkinje cells contacted by the same climbing fibre also increased. In principle, both numbers were the same. If, for example, the on-off signals in the olivary nucleus produced 6 climbing fibres per joint (as shown in the figure), there were also 6 Purkinje cells per climbing fibre that were excited by each of these climbing fibres. There are many reasons for this. One main argument is the formation of the mossy fibre projection into the spinocerebellum.

From the outset, the output of the spinocerebellum had the task of supplying the muscles with contraction signals. The output signals ultimately had to reach the motor output nucleus of the brain, i.e. the red nucleus. They travelled upwards from the cerebellar nucleus to the (motor) frontal cortex and, with the help of class 3 neurons, switched to the sensory side of the frontal cortex. There, the sequential signal divergence of the climbing fibres was reversed by signal convergence. As a result of this cortical signal convergence, there are now exactly as many class 5 cortical projection axons as there are divergent neurons in the olivary nucleus. However, since there is ultimately only one on-signal and only one off-signal to each simple joint ( ), a further, final signal convergence takes place in the red nucleus to restore this on-off signal pair. This signal pair now controls the two muscles, the flexor muscle and the extensor muscle. In addition, this on-off neuron pair projects back into the olivary nucleus, creating a kind of signal loop in which these signals constantly rotate and ensure that these two muscles do not lose their tension and that the set joint angle is maintained until additional signals enter this signal loop.

The signal convergence creates an area in the red nucleus with larger neurons whose dendrite trees must be quite large in order to combine the signals from the many axons for signal convergence. This magnocellular part of the red nucleus was noticed by neurologists quite early on.

In the motor cortex, the signal convergence also leads to the formation of output neurons with a larger dendrite tree. We will encounter these much later as Betz giant cells.

A special feature without which this circuit would not function must be explained. In the cerebellar nucleus, not only is the signal strength inverted, but also the on-off marker concentration. The two markers are (in principle) assigned to the two halves of the body. The formatio reticularis forms a strong signal mean value from the signals on each side of the body, taking a maximum of the respective body marker. This marker concentration reaches the cerebellar nucleus via the axons and there amplifies the maximum value of this body marker in each output neuron. The additional input via the climbing fibres, which also carry a marker concentration, reverses the on-off situation, resulting in a marker inversion.

This reverses the marker ratio in the mossy fibres and the cortical projection axons. Only then is a complete signal cycle established, in which the signal values of the individual climbing fibres, cortical fibres and mossy fibres remain stable and constant without additional external signals.

If you compare the input of the olivary nucleus with the input of the rubra nucleus, you will see that the signals are "swapped". This is because the output of the olivary nucleus is minimum-coded and inverted in the cerebellar nucleus, and is therefore subsequently maximum-coded. In principle, therefore, a kind of signal rotation must be performed so that the output of the nucleus ruber corresponds to the original input of the nucleus olivaris. This signal rotation is prepared by inverting the strength of the on-off markers in the cerebellar nucleus.

This signal rotation is also necessary because the motor cerebellar output always controls the antagonist muscles. Therefore, the output signal of the tendon organs of a flexor muscle is always fed to the muscle plate of the corresponding extensor muscle. This remains the case even after the signal divergence begins.

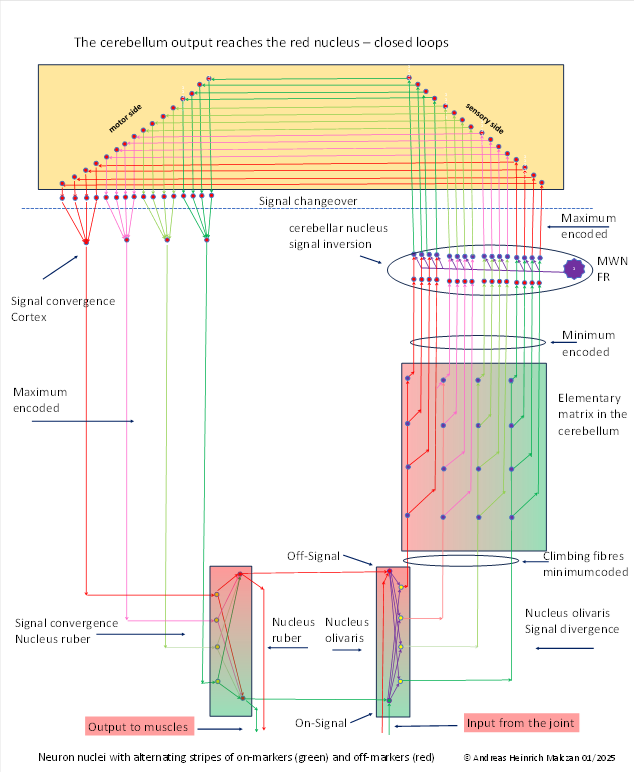
The cerebellar nucleus requires a strong mean signal from a mean neuron (MWN) of the formatio reticularis (FR) for signal inversion.

In this monograph, we will refer to each rectangle in which all Purkinje cells without exception receive input from a single joint as an elementary matrix (and later as a cluster). The reason for this is that the input originates from the same elementary signal, from whose on and off variants the input of the climbing fibres of this elementary matrix results through signal divergence. Instead of a (dual on-off) joint signal, any other elementary signal can also form such an elementary matrix (visual signals, acoustic signals, tactile signals, etc.). It only needs to be present in its dual form as an on-off signal. It is important that the number of climbing fibres in each elementary matrix is identical to the number of Purkinje cells present in each climbing fibre. Therefore, there are n² Purkinje cells for n climbing fibres.

In the figure above, each elementary matrix consists (for example) of 16 Purkinje cells and 4 climbing fibres.

For later use, we will adopt a convention for the elementary matrix. We will also refer to the columns of the matrix as climbing fibre columns, since all Purkinje cells arranged in them receive input from exactly one climbing fibre.

The 16 Purkinje cells of an elementary matrix form 16 output axons that travel to the corresponding cerebellar nucleus, where they inhibit 16 output neurons, which in turn are excited by mean signals from the formatio reticularis (and later by other signals). This results in signal inversion. Each of the 16 Purkinje signals of an elementary matrix is inverted in the cerebellar nucleus. Thus, each elementary matrix generates 16 output signals of the cerebellum, which travel to the cortex, whereby they must pass through the signal crossing in the brain.

Of course, we may ask ourselves why these cerebellar signals travel to the cortex. Before signal inversion, they travelled via the red nucleus to the antagonist muscles. But after signal inversion, there were many more motor signals than muscles. Most of them no longer had direct motor targets. These signals therefore found their way upwards to the frontal cortex, which did not exist before. The frontal cortex, in conjunction with the red nucleus, was able to reverse the signal divergence and thus recover the original motor signals.

The extreme value-coded cortex signals, which were then subjected to an initial signal convergence, behaved at some point in the course of evolution in the same way as the original cortex signals: they moved downwards in a " " direction towards the trunk, finding their way into the basal ganglia system via the substantia nigra pars compacta, among other places. They were also able to form a pathway to the limbic system and participate in signal rotation in the newly formed Papez circuits. However, the formation of a new projection back to the spinocerebellum was very important. This projection is called the mossy fibre projection.

The maximum-coded signals from the cortex, which received them from the cerebellum, first changed sides to the other side. To do this, they travelled along axons to the pontine nuclei and from there to the cerebellum, towards their original point of origin. The mossy fibre system is based on this signal projection. The mossy fibres transmit the input coming via the pontine nuclei to the cerebellum. In doing so, they must pass through the brain's signal crossing and change sides of the body. This change of sides is only symbolically indicated in the following illustration.

The existence of bridge nuclei is not confirmed in all vertebrates. It seems that they are only clearly discernible in birds (according to Gerhard Roth), although mammals also possess them. It is possible that they are only rudimentary in fish and reptiles, i.e. still in the process of development. The reason for this is explained later in this chapter.

     

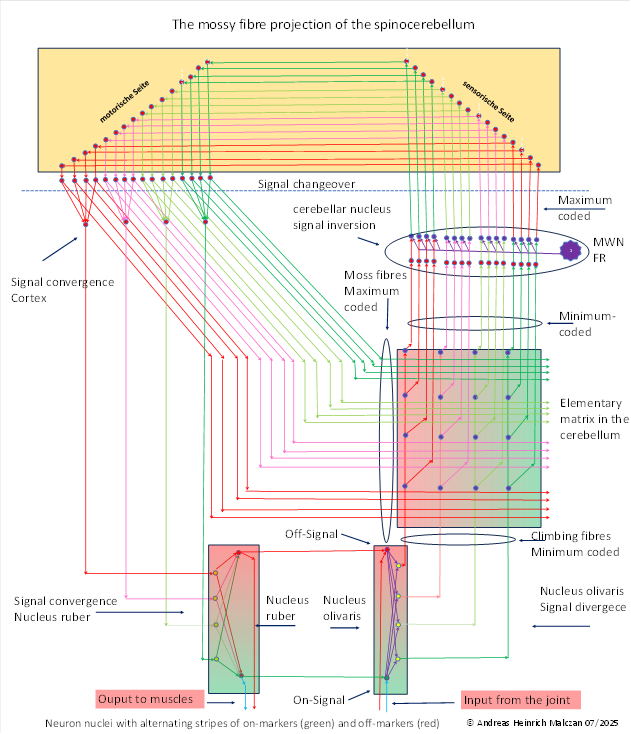
We now assume that the moss fibres reach us from the left in the figure above. We had assumed that the neural flat cables of the various elementary matrices are arranged in stacks and follow the topology of the marker concentration. Each flat cable made up of axons runs exactly to the rectangle in which the elementary matrix of Purkinje cells assigned to it is located. This is its original place of origin. Each axon of the mossy fibre, regardless of its marker concentration, finds its way to the elementary matrix from which it originally originated in the cerebellum ( ). Since there is a grouping within these mossy fibres according to marker concentrations (represented by different colours), we again assume that mossy fibres with the same marker concentration remain spatially together and do not mix with mossy fibres of other marker concentrations.

This way, the spinocerebellum gets its own output back through the mossy fibres, which go through the cerebellar nucleus, the thalamus, the cortex, and the pontine nuclei (some other nuclei are also involved, like the torus semicircularis or the tectum opticum).

Each mossy fibre signal finds its way to the exact elementary matrix from which it originated. We assume that this is controlled by additional marker substances, which we could call organ markers if we consider each joint as a separate organ. Each elementary matrix receives its own output as input.

The signals of the mossy fibres take on the marker topology of the original Purkinje cells from which they were derived. Therefore, the mossy fibres also form a neural flat cable to an elementary matrix, which has the same marker topology as the Purkinje axons. However, unlike the climbing fibres, the corresponding signals of the mossy fibres belonging to an elementary matrix are maximally coded, with one mossy fibre in each flat neural cable being most strongly excited.

Since the mossy fibres run orthogonally to the climbing fibres and have their own marker topology, there must be some kind of barrier between the data cables of the climbing fibres and those of the mossy fibres that hinders the diffusion of the marker molecules.

The original minimum coding of the climbing fibres was inverted in the cerebellar nucleus and therefore maximum-coded, which was passed on to the mossy fibres via the cortical projection and the projection via the pontine nuclei.

It is now generally known (hopefully) that the climbing fibres run orthogonally to the mossy fibres and also to the parallel fibres. This is the evolutionary legacy from the early days of cerebellum formation.

Originally, both halves of the body were in neural competition with each other. Each red nucleus projected via the lateral nucleus (nucleus olivaris) excitatorily into the red nucleus of the contralateral side of the body in inhibitory interneurons.

The projection axons used formed a right angle with the vertical body axis. Both the input axons and the output axons of the olivary nucleus (the lateral nucleus) ran orthogonally to the body axis. This remained the case even when the inhibitory interneurons of the contralateral red nucleus separated into an independent nucleus, which later developed into the Purkinje nucleus of the cerebellar cortex. The signals descending vertically from the cortex (after a lateral shift) towards the trunk came from above and passed downwards past the cerebellum, where they came into spatial contact with the Purkinje cells. Here, the climbing fibres from the olive ran orthogonally to the descending cortex signals. Climbing fibres and mossy fibres have therefore run orthogonally to each other since time immemorial. The parallel fibres derived from the mossy fibres took over this orthogonality, which we can still observe today.

The orthogonality of these two fibre systems was an essential prerequisite for the emergence of intelligent behaviour and later for mental intelligence. This is explained in this chapter and clarified later.

For the spinocerebellum, analysis of its neural circuitry provides insight into an unusual and completely new type of signal processing. Initially, it seemed that the main task of the spinocerebellum was to invert motor signals in order to obtain control signals for the motor antagonists. However, signal divergence and orthogonality between climbing fibres, mossy fibres and parallel fibres revealed that the spinocerebellum is capable of much more and can perform signal analysis, which the author found in primates.

In chapter "4.2. Divergence modules with lateral signal propagation" of this monograph, I described the theory of divergence modules with lateral signal propagation. This explained, for example, why an excitation maximum in the cortex wandered around a circular line when the monkey moved its arm in a circular lifting motion in an experimental setup. Its brain converted the periodic movement of the arm into a periodic movement of the cortical excitation maximum.

I was also able to show that in the visual domain, divergence modules with lateral propagation cause periodic movements of a rotating straight line in the visual field to produce periodic movements of a corresponding excitation maximum in the visual cortex.

Once I had recognised this analytical property of divergence modules in principle, the question arose in my subconscious as to how birds, for example, could analyse periodic movements of the body or visual objects. According to my theory of the DVR and the hyperpallium ( ), they did not have divergence modules with lateral signal propagation. Their brains did not have cell columns like the primate cortex. Nevertheless, birds prove every day that they are capable of analysing periodic processes. Their flight alone is the result of the analysis of all periodic movements associated with bird flight.

So the search began for the cause of this analytical ability in birds. Since, according to all experts, the spinocerebellum is responsible for fine motor coordination, there had to be a signal analysis hidden in the spinocerebellum that needed to be found.

The search was successful on 20 January 2025 and revealed a completely hidden algorithm for the signal analysis of periodic signals. This resulted in Chapter 20, entitled "The connectome of the spinocerebellum". However, it took another six months to iron out the last inconsistencies and completely rewrite this chapter in its current form.

When a mossy fibre projection established itself in the spinocerebellum, the cortex signals of the mossy fibres were able to connect with the signals of the climbing fibres and interact with each other. Further above, especially in the illustration, it was made clear that it is essentially the same signals that reach the spinocerebellum via both the mossy fibres and the climbing fibres. This is an extremely important insight that brings us closer to solving all questions about the spinocerebellum.

Let us go back to the beginning, when the mossy fibres and climbing fibres first established contact. The Purkinje cells already existed and received input from the climbing fibres. They only had synaptic contact with a single climbing fibre; there were no large dendrite trees. Now let's move forward in time to when signal divergence developed in the olivary nucleus. The dendrite trees of the Purkinje cells began to form, initially quite small and round. This brought them close to the mossy fibres passing through this area. If n signals derived from an on-off signal pair arose in the olivary nucleus through signal divergence, and each resulting climbing fibre contacted n Purkinje cells in the cerebellum, there were n² Purkinje cells. The number of Purkinje cells grew quadratically with the degree of signal divergence. Similarly, the number of mossy fibres also grew quadratically with the degree of signal divergence. Therefore, the dendrite trees of the Purkinje cells had to grow along with them, becoming larger and ultimately extremely large. However, the axons of the granule cells, which as interneurons transmitted the mossy fibre excitation to the Purkinje cells, also had to become longer, as the number of Purkinje cells to be reached increased with the degree of signal divergence.

Synaptic contact was established by granule cells. We consider these to be the interneurons of the cerebellum.

The principle was quite simple:

Each mossy fibre signal inhibited the Purkinje cells reachable by its axon if the mossy fibre signal was not identical to the signal from the Purkinje cell. Neuronal simplicity: "Inhibit all foreign signals".

Now we just need to clarify what foreign signals are in the cerebellum.

Here, the principle of signal similarity applies. This applies to on-off signals that emerge from each other through signal inversion. They are (in the first stage) signal-similar. All signals that emerge from each other through signal divergence are also signal-related. This means that all signals in a neural data cable of the olivary nucleus are signal-related to each other if they arise through signal divergence. Of course, this signal relatedness decreases the further the signal divergence progresses in the olivary nucleus.

A tool for determining signal similarity in the cerebellum could be the ratio of on-off markers, which maintain topological order in the cerebellum.

Let us now return to the spinocerebellum and its structure consisting of elementary matrices. In this case, all signals of an elementary matrix are signal-related to each other. Therefore, they will not form any contacts with each other (at this stage of evolution!). The Purkinje cells will not form any synaptic contacts with mossy fibres whose signals originate from this elementary matrix. This is especially true in the early phase of the cerebellum; much later in evolution, this rule was modified because the input signals underwent a modification (transition from elementary signals to mean signals). A violation of this rule from the early days of the cerebellum would have meant that a Purkinje cell would have been excited by the input from the mossy fibres of its own elementary matrix. Since both signals were inverse to each other because the climbing fibres were minimally coded and the mossy fibres were maximally coded, a superposition of both excitations would have resulted in a constant corresponding to the maximum firing rate, which would have led to damage to the neural circuit (overload) in a very short time.

But what happens if the mossy fibre signals originate from a neighbouring elementary matrix? This is where neural competition comes into play. The Purkinje cells of an elementary matrix are inhibited by all mossy fibres reaching them when these signals arrive from a foreign (neighbouring) elementary matrix. This is how neural competition works in the brain!

In order for the Purkinje cells of an elementary matrix to receive the mossy fibre signals from a neighbouring elementary matrix, interneurons must enable this signal transmission. These interneurons were the granule cells. However, if a granule cell wanted to perform the task of inhibiting the Purkinje cells of the neighbouring matrix, it had to allow its axons to grow towards the neighbouring matrices. And because the granule cell signal was a foreign signal to both neighbouring matrices, the axons had to grow both to the left and to the right, developing considerable length in the process. The further the signal divergence progressed, the wider (and higher) the elementary matrices in the cerebellum became, and the longer the parallel fibres had to become in order to reach neighbouring elementary matrices.

This resulted (in the course of evolution) in the typical T-shaped structure of the axons of the granule cells, which are called parallel fibres and run vertically to the climbing fibres. They transmitted the foreign signals to the neighbouring elementary matrices. Foreign signals inhibit the Purkinje cells located there. This is the signal principle of the spinocerebellum. Since the mossy fibres formed considerable neural data cables, which were also stacked on top of each other, the axons of the granule cells first had to rise vertically upwards until they had crossed these rather thick stacks of data cables made of mossy fibres; only then could they branch off to the left and right in a T-shape. We refer to these axons as parallel fibres. The data cables of the output signals should also not be forgotten, as their number also increased quadratically with the degree of signal divergence. The climbing fibre axons also ran there and formed a data cable.

The T-shaped branching of the grain cell axons did not necessarily occur in all vertebrates. Gerhard Roth (born 15 August 1942; died 25 April 2023), one of Germany's most important brain researchers, describes an exception to this in the publication "The granular layer of the mormyride cerebellum: lateral arrangement relative to the molecular layer", Roth G. & Diecke F.P.J. (1978), Anatomischer Anzeiger 141(3): 150–166. In mormyrids (also known as Nile loaches), the granular layer is located in the cerebellum, more precisely in the vulvula cerebelli, not below but to the side of the molecular layer. The grain cells send their axons parallel to the surface and are not T-shaped. This cerebellum structure serves to evaluate mechanoreceptive and electroreceptive signals. These fish can analyse their environment with the help of self-generated electric fields and develop huge cerebellum structures for this purpose.

The significance of Gerhard Roth can undoubtedly be compared to that of Charles Darwin. Charles Darwin recognised the evolution of species and thus established a completely new view of the development of life. Gerhard Roth recognised the evolution of brains and showed that there was a continuous, progressive development of nervous systems in vertebrates. My monographs describe and analyse precisely this evolution from a signal theory perspective.

But now let us move on to signal divergence, which also occurred in vertebrates in the course of evolution. It most likely began in those neural structures that are considered evolutionary novelties. The nucleus olivaris, part of the side-shifting system, which completed the transition from contralateral inhibition to contralateral inverse excitation, culminating in the development of the cerebellum, is a candidate for this.

Initially, signal divergence in the olivary nucleus was still low, so that there were only a few climbing fibres and just as few mossy fibres. At that time, the elementary matrices in the cerebellum were still quite small. Therefore, the axons of the granule cells were quite short. Only with the increase in signal divergence did the ever-larger elementary matrices expand spatially, so that the axons of the granule cells, the parallel fibres, had to become longer and longer if they wanted to reach a neighbouring elementary matrix. We must imagine the increase in length of the parallel fibres, which are actually the granule cell axons, as a dynamic process. With the quadratic increase in the number of Purkinje cells and mossy fibres, the dendritic trees of the Purkinje cells also had to grow, eventually reaching enormous proportions in primates.

In order for the parallel fibres of the body cells to inhibit the Purkinje cells, they had to enlist the help of interneurons, which are called stellate cells in the cerebellum. The parallel fibres of the foreign matrices excited these stellate cells. The stellate cells inhibited the Purkinje cells. In this way, an elementary matrix inhibited its neighbours.

These findings provide a good explanation of how the spinocerebellum works in principle, but above all they show the enormous advantages that the spinocerebellum offered in the struggle for existence.

This explanation will now be provided. As the author who developed this theory of the cerebellum, I claim the copyright for it.

We will focus on motor function, even though the analysis of other modalities such as sight, smell or taste was similar. In the very early stages of evolution, animals swam in the primordial ocean. If they happened to encounter food, they ate it. A targeted movement towards food would be an evolutionary advantage in the struggle for existence.

We want to prove that the spinocerebellum was already helpful in the search for food at a very early stage because it facilitated a targeted analysis of motor skills.

Let us imagine a simple vertebral joint. It allows the spine to bend (slightly) in any direction. If, in early evolutionary times, a fish was able to control the curvature of its spine with the help of visual prey signals in such a way that forward movement led it directly to its prey, it had a great evolutionary advantage in actively pursuing its prey. But to do this, it had to be able to determine the angles formed by its vertebral joints. It needed a "concept" of its body, comprehensive information about itself. The spinocerebellum made this possible through comprehensive signal analysis.

The mobility of the spine is made possible by facet joints.

We imagine such a joint with two degrees of freedom. It should allow movement in two planes that are perpendicular to each other. In one plane, the angle α may denote the deviation from the centre position, and in the other plane, it may be the angle β.

In a fish, angle α could indicate the deviation from the body axis in the vertical direction (raising or lowering the head), while β determines the deviation in the horizontal direction (moving the head to the left or right).

We imagine the tectum opticum of the fish (simplified) on the sensory side as a circular area of neurons that receive input from the equally circular retina. There, the neural image of a small prey fish can be seen. The retinal neurons (ganglion cells) transmit the visual image of the prey in signals consisting of firing rates.

If the prey fish is in front, its neural image is in the centre of the tectum, otherwise it is off-centre, with angles α and β determining the deviation from the centre. In the area of the neural image, the tectum neurons fire and signal: "The prey is here!"

The fish will swim towards the prey if its spine curves at exactly these angles α and β, so that forward movement leads to the target, because the fish will then "collide" with the prey fish and be able to eat it.                

How can the spinocerebellum determine these angles? And how can it convert the joint angles α and β involved into a flat image similar to the tectum so that the image of the fish can interfere with the image of the joint angles via interneurons? How can the image of the prey influence the flat image of the joint angles?

We need a representation of the two joint angles in the plane. Mathematically, this is a function of two variables!

Back to the vertebral joint. Let us assume (for simplicity) that it is controlled by four muscles (later by four muscle groups). The first two muscles change the joint angle α by contracting. The other two muscles cause a change in the angle β. One muscle is the flexor muscle, the other is the extensor muscle.

There are a total of four muscle signals with the corresponding firing rates: f_α , f_α^* , f_β and f_β^* . The asterisk denotes the firing rates of the extensor muscles, which are inversely proportional to the firing rates of the flexor muscles. Thus, two firing rates form an on-off signal pair, one for angle α and one for angle β.

The on-off signals of the joint angle α may reach the olivary nucleus, where they are transformed by signal divergence into a minimally coded neural data cable, which reaches the elementary matrix A in the spinocerebellum via n climbing fibres. Each climbing fibre contacts n Purkinje cells of the elementary matrix A, so that a total of n² Purkinje cells are required. The output of these n² Purkinje cells travels via a stack of n neural data cables to the cerebellar nucleus. This cerebellar output is inverted in the cerebellar nucleus and is therefore maximally coded. It travels upwards to the cortex, from there back via the pontine nuclei and reaches a stack of n maximally coded data cables via the mossy fibres of the same elementary matrix. The mossy fibres are rearranged in the cerebellum according to their on-off marker ratio.

The same happens for the joint angle β, but the data cables end in a neighbouring elementary matrix B of the cerebellum.

Since the signal-transmitting muscle spindles of the joint under consideration are spatially close to each other (they belong to the same body segment, for example), the on-off signals of the angle β will reach the cerebellum in the elementary matrix B after signal inversion in the olivary nucleus. This is the right-hand neighbouring matrix of matrix A. Thus, both elementary matrices are directly adjacent and can exchange their signals via their mossy fibres with the help of the granule cells and their parallel fibres.

According to our considerations, matrix A will inhibit matrix B via the parallel fibres, and matrix B will inhibit matrix A in the same way.

In both cases, the climbing fibres in matrix A and also in matrix B are minimum-coded, since the supplying neural data cables for each of the two joint angles are also minimum-coded.

The parallel fibres are maximally coded. The reason for this is the signal inversion in the cerebellar nucleus. The own parallel fibres have no effect in the elementary matrix A or B. However, the foreign parallel fibres from the neighbouring matrix inhibit the Purkinje cells. This is because foreign signals cause neural competition.

It should also be noted that not every parallel fibre of the neighbouring matrix can inhibit the Purkinje cells of a matrix. This is because the axons of the mossy fibres form a topologically well-sorted flat cable in which there is an on-off mixing ratio of the markers orthogonal to the data direction, which is caused by the on and off markers in the olivary nucleus. Therefore, a parallel fibre in the elementary matrix only contacts Purkinje cells in a row, as the mossy fibre is bound to the on-off marker ratio. The axons with the foreign signals from the neighbouring matrix cannot leave their horizontal position within the associated data cable. Thus, a mossy fibre only contacts the Purkinje cells in its row via its granule cells.

The "parallel" course of many signal lines in the human brain has been impressively demonstrated by American researchers in the Human Connectome Project. There, it can be seen that the fibre course of the axons in the brain is basically organised in a non-crossed manner; the fibres do not mix as they travel from one place to another. We see something similar in the figure above and attribute this peculiarity (among other things) to the existence of markers that control the course of the fibres.

We will now discuss the superposition of the neural excitations of the climbing fibres and the mossy fibres (parallel fibres) in an elementary matrix of the cerebellum. To do this, we will use an excerpt from the previous figures. In this example, we use a signal divergence on 6 climbing fibres. In the elementary matrix of the cerebellum, 36 Purkinje cells are activated, which in turn activate 36 output neurons in the cerebellar nucleus, so that a total of 36 mossy fibres return to the cerebellum via the cortex and the pontine nuclei. The neighbouring matrix also includes 36 mossy fibres, on which the foreign signals arrive via granule cells and their relatively long parallel fibres in the elementary matrix under consideration.

First, we look at the excitation contribution that the climbing fibres supply to the Purkinje cells. It is constant in the y-direction (here vertical), but has a minimum in the x-direction (horizontal), whose position x_min  encodes the joint angle α. We illustrate this with an example graph.

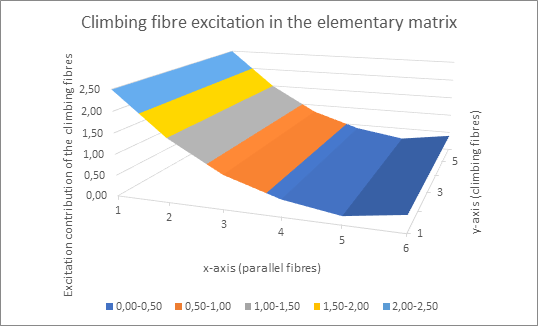
It can be seen that in the above example, climbing fibre no. 5 provides the lowest excitation contribution, because there is a global minimum for x = 5. This applies to all values of y.

We define a new class of functions. Let f(x) be a function of the variable x. Then we denote the function

as the trivial continuation of the function in the direction of y.

Then we can formulate the following with regard to the climbing fibres:

The climbing fibres realise the trivial continuation of the climbing fibre excitation in the direction of the climbing fibres with their axons.

Each climbing fiber transports its own excitation in the direction in which it propagates:

.

The global minimum x_min  is passed on in the trivial continuation in the y direction.

The parallel fibres run in the x direction. In the x direction, the function values are constant for each value of y. In the y direction_, the excitation of the parallel fibres has_a maximum y(_max). Since the parallel fibres transmit the excitation of the neighbouring elementary matrix (here from the right), they have an inhibitory effect as foreign signals. They excite star cells, which in turn inhibit the Purkinje cells of the elementary matrix.

The mossy fibres with the connected granule cells use their axons, the parallel fibres, to carry on the mossy fibre excitation in the parallel fibre direction.

The strongest inhibitory effect occurs where the parallel fibres have the greatest excitation, i.e. an excitation maximum.

The superposition of climbing fibre excitation and parallel fibre inhibition leads to a two-dimensional excitation function in the area of the elementary matrix, which has exactly one global minimum at the point P(x_max, y_max).

Since one excitation component of the climbing fibres represents a trivial continuation in the x direction according to the formula

,

while the parallel fibre excitation is a trivial continuation in the y direction according to the formula

,

the superposition of the exciting climbing fibre signals with the inhibiting parallel fibre signals of the neighbouring matrix results in the sum

.

This total excitation of the Purkinje cells is a function of x and y. However, we have a separation of variables here. This means that the global extreme value (if it exists) is identical to the extreme values of the two initial functions. The x-coordinate of the global minimum is identical to the x-coordinate of the climbing fibre excitation, and the y-coordinate of the minimum is identical to the parallel fibre excitation. This is caused by the fact that the derivative of zero is zero. Each coordinate has a function value of zero.

The global excitation minimum in the elementary matrix thus encodes the two joint angles α and β. The Purkinje cell belonging to the point P(x_max , y_max ) (or the one closest to this point) encodes the sizes of these two joint angles of the rotary joint. It has the lowest firing rate. This signal is transmitted along its axon to an output neuron of the cerebellar nucleus, where the signal value is inverted. Thus, the original minimum becomes a maximum.

The elementary matrix thus represents a coordinate system in which the x-axis represents the angle α and the y-axis represents the angle β ( ely, however, on a non-linear scale). In the z-direction, we can imagine the excitation of the associated Purkinje cells, which are distributed there in a grid pattern. The global excitation minimum at point P(x,y) uniquely encodes the current values of the angles α and β.

This achieves our goal: the two joint angles of a vertebral joint are represented in the plane as a function and can now interact with the prey image of the tectum opticum.

Since all output neurons of the cerebellar nucleus project into the cortex, there is a signal image of the cerebellar elementary matrix, which we can refer to as the cortical elementary matrix. It encodes the two joint angles α and β via the position of the global maximum in this area. The maximum excitation results from the signal inversion of the minimum excitation in the cerebellar nucleus.

If the joint angle α is now changed, the minimum excitation in the cerebellum or the maximum excitation in the cortex moves back and forth in the x-direction, resulting in a horizontal movement of the extreme value. If the second angle β of the joint is changed, the extreme value moves back and forth along a vertical line. In the functional representation, both angles are also orthogonal to each other.

If the two joint angles belong to an arm that performs circular movements, the extreme value in the cerebellum and in the cortex will move along a circular line. The size of the circle will depend on the arm rotation. If the arm rotates in small circles, the image of the movement in the cerebellum and cortex will consist of small circles. If the arm rotates in large circles, the extreme value in the cerebellum and cortex will also do so in large circles.

And because the signals ascending from the cerebellum to the cortex must pass through the structure of the optic tectum (among other places), the tectum signals (the prey image) can influence these cerebellum signals by transmitting their excitation to them via interneurons, thereby influencing motor function. As in a power steering system, the prey will control the muscles in such a way that the image of the joint angles (the maximum motor excitation) approaches the image of the prey in the tectum until both coincide. Now all that remains is a forward movement towards the prey and it can be eaten.

So far, we have described the tectum opticum as an approximately circular area. This will only be the case in higher vertebrates (see Chapter 3, "The change in image topology and the transition from cylindrical to spherical body models" in this monograph). In the early days of the " " (spinning-top body), all body models, including the tectum opticum, had a fundamentally cylindrical shape, which resulted from the shape of the neural tube. Here, the spinocerebellum was able to control the curvature of the spine via a neural tube projection. To this end, we imagine the x-y plane of climbing fibres and moss fibres arranged so that it is perpendicular to the body axis, with the x-direction running horizontally and the y-direction running vertically. If the extreme point P(x(_{max) ;}y(_max))is connected to the zero point, a vector is created whose direction corresponds to the direction of the body curvature. A circular rotation of this vector would indicate a circular change in the body curvature. If this circle is ideally mapped onto the hollow neural tube, with the projection only taking place in the sensory half-cylinder, the cortical output neurons only need to be mapped in an orderly manner onto the sensory half of the neural tube. Control is then also possible if the body models are arranged in a cylindrical shape (one sensory and one motor half-cylinder each).

The joint angle analysis of joints with two degrees of freedom is an excellent body analysis made possible by the spinocerebellum. It corresponds roughly to what flat divergence modules can achieve, as described in chapter "4.2. Divergence modules with lateral signal propagation" in the monograph "Human Brain Theory" (link: https://www.gehirntheorie.de/Kapitel-4-2.html).

However, we are dealing here with linear signal divergence in the olivary nucleus, the early form of all signal divergences. We call it linear because the output signals propagate along a line. It is generally minimum-coded. Maximum-coded signal divergence in the area probably only developed in primates. Early vertebrates had to resort to minimum-coded signal divergence with the classic cable equation for myelin-free axons, but were able to analyse the signals quite well with this. As a result of minimum coding, they must use the spinocerebellum for signal inversion. There, signal divergence and the orthogonality of climbing fibres and mossy fibres (parallel fibres) lead to the desired body analysis.

If the neurons involved were part of a neural network that receives input from the olivary nucleus, it would be virtually impossible to determine the associated joint angles α and β with so few neurons and represent them as a function of two variables in the plane.

Furthermore, it should be noted that the circuitry of the elementary matrices in the cerebellum and cortex does not require any learning processes whatsoever. At the described stage of development of the spinocerebellum, no learning is required for this signal analysis!

It is imperative to dispel the myth that the entire brain is a learning neural network. Large parts of the brain are used for signal analysis and perform intelligent tasks without Hebbian learning or LTP or LTD. They perform exactly the same tasks that signal analysis and signal processing perform in deep neural learning. This is because even artificial neural networks are not fed with original data (e.g. photos, sound, encyclopaedias), but rather this data must first be processed at great expense and converted into the correct data format. This already requires enormous computing power. It is no different in the brain. Large parts of the brain are used for data processing. This does not require any learning processes, no Hebbian learning, no LTP or LTD, but only mathematically based algorithms that need to be identified and that are usually successfully hidden in the neural circuits.

The reader was promised an answer. Why do fish have no or only rudimentary pontine nuclei and therefore no or only very low mossy fibre projection into the spinocerebellum?

The reason is simple: fish have only two muscles per vertebral joint that set the joint angle α. They cannot set a second angle β because they lack the necessary muscles. Therefore, they do not need an elementary matrix that can analyse the relationship between angle α (left/right) and angle β (up/down). The second angle does not exist. Their vertebral joints have only one degree of freedom. Their spinocerebellum is therefore very simple in structure. For each vertebral joint, there is an arc of a series of Purkinje cells that analyse the joint angle of this vertebra in a minimum-coded manner. There is one such series of Purkinje cells for each vertebral joint. In addition, there are such cell rows for the fin joints. Each Purkinje cell row sends its output signals via the cerebellar nucleus to the cortex, where they switch to the motor side and descend to the red nucleus. There, the signal divergence is reversed. A cortical bridge core projection is not necessary as it serves no purpose.

Amphibians have four muscles per vertebral joint, i.e. two pairs of muscles, and can therefore analyse their vertebral joints in two degrees of freedom. They already use the elementary matrices in the spinocerebellum. For each vertebral joint, there are two elementary matrices, which (probably) each form a cerebellar arch consisting of n columns of Purkinje cells supplied by the same climbing fibre. They are arranged in an arch shape because the Purkinje cells need more space on the outside than on the inside, where the cell bodies, climbing fibres and mossy fibres are located. A cerebellar arch consists of n such columns lying next to each other. In principle, the two elementary matrices are curved outwards in the form of cylinders. This arrangement is found for each vertebral joint. In addition, there is an analogous cerebellar system for the joints of the extremities.

Reptiles already have three pairs of muscles per vertebral joint, i.e. 6 muscles per vertebral joint. In their spinocerebellum, there are therefore three elementary matrices next to each other per vertebra, which together form three cerebellar arches lying next to each other. These three cerebellar arches exist for each vertebral joint, so that their number should be determinable. In addition, there are similar arches for the extremities.

Mammals already have four muscle groups per vertebral joint, i.e. a total of eight muscles. In their spinocerebellum, there must therefore be four elementary matrices per vertebra, which also form four cerebellar arches lying in a row. There are as many rows of these as there are vertebral joints. In addition, there is a corresponding cerebellar structure for the limb muscles.

One might think that this fully explains signal processing in the spinocerebellum. However, this is not the case. There are other interneurons in the cerebellum that have not yet been discussed here: the Golgi cells and the basket cells. Other interneurons are also known, but the author has not yet completed his theory on this.

The tasks of interneurons can be most easily explained by their transmitter and their interconnection, whereby the principles of excitation and inhibition must be taken into account.

Interneurons with excitatory transmitters collect neural signals and pass them on. Interneurons with inhibitory transmitters also collect neural signals and pass them on.

There can be two different reasons for inhibition:

-         Either competing signals are inhibited, which serves to enhance contrast.

-         Or signal averages are inhibited in order to invert signals, i.e. to reverse their signal strength ratio. Inversion neurons either require external average signals or generate these themselves by tapping into the (exciting) signals passing through their area. To do this, they need larger dendrite trees.

Statistically speaking, the inhibition of competing signals is more common. Neuronal competition between signals is a preferred way of giving greater weight to stronger signals. This allows the brain to focus on what is essential. This approach will help us understand the role of basket cells and Golgi cells in the spinocerebellum. However, the role of these cells in the pontocerebellum may be different, as the pontocerebellum receives different types of signals as input.

First, let us recall that the spinocerebellum is part of the secondary brain system. It generally receives pairs of on-off signals from the primary brain system, each of which is inverse to the other. Both are analogue signals whose signal strength is transformed into a firing rate. There is signal competition between these signals, which we will refer to as primary signal competition. It is passed on in the cerebellum to the two associated, neighbouring elementary matrices. Therefore, the signals from one elementary matrix inhibit the associated, neighbouring elementary matrix. This happens when the mossy fibres, which each terminate in the area of the associated elementary matrix, contact and excite granule cells. Their axons ascend, branch out and form parallel fibres. Due to their great length, these fibres reach the associated neighbouring elementary matrix, where they inhibit the Purkinje cells via intermediate star cells. This ensures primary signal competition between these two elementary matrices. Each elementary matrix inhibits its associated neighbour.

The output of the spinocerebellum represents signals from the secondary system. Here, too, a secondary signal competition develops in the course of evolution, in which the signals of one and the same elementary matrix compete with each other. Due to the special structure of the cerebellum, two types of interneurons involved in secondary signal competition develop. Secondary signal competition in the spinocerebellum is realised (according to the author of this monograph) by the basket cells and the Golgi cells. The basket cells realise secondary signal competition in the y-direction, i.e. in the direction of the climbing fibres. The Golgi cells realise secondary signal competition in the x-direction, i.e. in the direction of the mossy fibres. In the climbing fibres, at a degree of divergence of n, there are exactly n climbing fibres that compete with each other. These give rise to n² mossy fibres, which are divided into groups of n mossy fibres with the same on-off marker ratio, each group competing with the others.

 

Let's start with the basket cells. They tap into the signals from the parallel fibres (i.e. the axons of the granule cells) and inhibit the Purkinje cells. Near a Purkinje cell, they unfold their larger dendrite tree and thus apparently receive parts of the input available there, which is also available to this Purkinje cell. Now let us remember that each Purkinje cell does not tap into parallel fibres whose signal originates from the same elementary matrix (intrinsic signal). Instead, the parallel fibres from the neighbouring matrix arrive and inhibit this Purkinje cell via intermediate star cells. It should be noted here that only parallel fibres with a uniform concentration of on-off markers from the neighbouring matrix are contacted and inhib , as these are also well ordered there according to a marker gradient. We assume that the basket cell whose cell nucleus is located near a Purkinje cell synaptically taps precisely these parallel fibres from the neighbouring matrix, paying attention to the on-off marker ratio. The excitation received now serves to inhibit all Purkinje cells in the relevant column. To do this, the basket cell forms a long axon, which divides into two axons that follow the course of the climbing fibre exactly. In this way, each Purkinje cell of this climbing fibre is inhibited by the aforementioned basket cell. To do this, the basket cell forms a basket-like axon network at each Purkinje cell it contacts, which wraps around the cell body of the respective Purkinje cell and thus causes quite strong inhibition. It should be noted that each Purkinje cell has a basket cell that belongs to it. Therefore, each Purkinje cell is inhibited by many basket cells whose axons wrap around the cell body of the Purkinje cell.

The orientation of these basket cell axons corresponds exactly to the course of the climbing fibres. We assume (hypothetically) that this increases the contrast. The excitation in this column of Purkinje cells is minimum-coded, but this minimum is always greater than zero. This minimum is now additionally inhibited by the basket cells. The reason for this is the excitation of these basket cells by the parallel fibres of the neighbouring matrix, whose foreign signal inhibits the intrinsic signal of this elementary matrix. If the resulting minimum coding in the y-direction (column direction) is to be enhanced, the dendrites of the basket cells must be excited by the foreign signal. If they now inhibit neighbouring Purkinje cells, the inhibitory effect of the foreign signal from the neighbouring matrix is strengthened. Ideally, the minimum then even assumes the value zero, so that the subsequent signal inversion in the cerebellar nucleus assumes the maximum value.

In principle, it is clear that the new signals (elementary signals) obtained through signal divergence compete with each other neuronally. In the y-direction, mutual inhibition is realised by the basket cells.

In the x direction, the neural competition between these signals is realised by the Golgi cells. Here I must correct my own earlier statements.

I used to assume that the Golgi cells were used to switch off the signals from the mossy fibres. This may (possibly) be the case in the pontocerebellum. However, I can no longer support this view with regard to the spinocerebellum. A comprehensive analysis of the neural circuitry of the spinocerebellum yielded a different finding: the Golgi cells amplify the signal contrast between the Purkinje cells in a row, i.e. in the direction of the mossy fibres. This must be explained.

We assume that (possibly only in primates) there is an associated Golgi cell in the vicinity of each Purkinje cell. Each Purkinje cell taps the signals of a group of mossy fibres with the same on-off marker ratio, which come from the neighbouring matrix as parallel fibres and inhibit this Purkinje cell. It is precisely these parallel fibres that excite the Golgi cell. However, its signal is in secondary signal competition with the signals from the other groups of mossy fibres. Therefore, this Golgi cell will form synaptic contacts with precisely these competing mossy fibres by docking at the contact points between these mossy fibres and the associated granule cells and forming inhibitory synapses there. The mossy fibre signals of a group with identical on-off markers inhibit all other groups with different on-off markers. This is how secondary signal competition is realised in the x direction, i.e. in the direction of the mossy fibres.

The number of basket cells and Golgi cells increased during evolution, and with it their inhibitory effect on competing signals.

Now we just need to explain why the elementary matrices (at this stage of evolution) generally occur in pairs.

We assume that the moss fibres originating from an elementary matrix generally end exactly in the area where this elementary matrix is located. This results in a unique projection of the cortex into the spinocerebellum. If the length of the parallel fibres takes into account the signal divergence that occurs, then a parallel fibre can at most reach the neighbouring matrix.

Let us consider the corresponding body model – for example, an amphibian in early evolutionary times. Unlike fish, amphibians already had four muscles per vertebral segment, i.e. the two pairs of muscles required for two related, neighbouring elementary matrices per segment. Fish could not use this algorithm because they only had one pair of muscles per segment. They therefore did not need bridge nuclei. The output of their spinocerebellum simply controlled the contralateral muscles. But now let's continue with the example of amphibians.

The body was segmented. Each segment of the trunk had exactly one vertebral joint. This projected into a segment of the early neural tube. Like the body, the corresponding cerebellum model was a kind of long tube (with ventricular fluid?), with one tube section for each segment. This contained exactly two elementary matrices of Purkinje cells, which belonged to this vertebral joint with two degrees of freedom. They were arranged side by side on this tube model, one elementary matrix on each half of the cylinder. We imagine this cerebellum cylinder for this segment. On one half was one elementary matrix, which was responsible for the raising and lowering of the head or the torso. On the opposite half of the cylinder was the second elementary matrix, which was responsible for lateral movement to the left or right. Each mossy fibre had to reach the neighbouring matrix with its signals. It could not leave its location because it was bound to an on-off marker concentration. However, the granule cell contacted by the mossy fibre could reach the Purkinje cells of the opposite elementary matrix with its axon. There were even two ways to do this. The parallel fibres only had to move to the opposite side on a semicircular path on the outside of the cylinder, and there were two possibilities for this. In principle, they met there, so that they did not have to grow any longer. The parallel fibres thus formed a right angle with the body axis (and with the climbing fibres moving into the cerebellum); this orthogonality had been present from the beginning. The more the signal divergence increased, the larger the diameter of this cerebellar cylinder became, which clearly belonged to the vermis cerebelli.

However, the tendon organs of the muscles, which measured changes in joint angles, were not the only receptors in this segment of the body. There were also tactile receptors, pain receptors and receptors that measured various body parameters of the life support system. These receptors (in the course of evolution) sent their signals via projection neurons and also via the mossy fibre projection to the spinocerebellum. There, the associated mossy fibres formed their own modality layers. In the spinocerebellum, these were also arranged in partial cylinders per segment (just like in the neural tube), with the different modalities forming nested cylinder rings. The mossy fibres formed synaptic contacts with associated granule cells, whose axons ascended into the Purkinje layer and triggered inhibition of the Purkinje cells via stellate cells. This caused the motor antagonist, an associated muscle controlled by the Purkinje cell, to contract. The additional inhibition of the Purkinje cell by the pain or touch signal prevented damage to the body, and the contraction of the antagonist muscle moved the segment away from the site of the dangerous influence. This is why, in addition to parallel fibres with motor signals, there are also parallel fibres with pain and touch signals and other modalities that could have a motor effect. This corresponded to the spinocerebellum's own apparatus.

However, there was a significant topological difference between the spinocerebellum and the neural tube: the neural tube was divided longitudinally into a motor and a sensory part. The spinocerebellum, which was also tubular, was only sensory and was essentially a body model of the equally elongated body. However, this model was layered in terms of its sensory modalities – this layering was evident in the layering of the mossy fibres.

The angle analysis described here was an important prerequisite for the gradual transition of primates to upright walking. At the latest after the transition from the cylindrical body models of the hollow neural tube to the spherical, almost flat and almost circular body models in the tectum opticum and torus semicircularis, the elementary matrices of the spinocerebellum were able to interact with the signals of the vestibular sense and ensure gait stability.

But development continued. An elementary matrix could only achieve a fairly low angular resolution. If, for example, the signal divergence in the olivary nucleus was of degree 8, there were exactly 8 climbing fibres for each on-off signal pair, each of which contacted 8 Purkinje cells. If the joint could assume an angle of 0 to 90 degrees, for example, this elementary matrix could recognise 8 partial angles, each of which was an integer multiple of 90/8. An angle interval had a width of 11.25 degrees. An angular resolution of 11.25 degrees is quite moderate, but already quite valuable in evolutionary terms.

If nature could develop a further level of angular resolution, the accuracy could be increased eightfold. Then the angle analysis had to be repeated recursively.

We know that for the elementary matrix (in our example), 8 climbing fibres were created per on-off signal pair through signal divergence in the olivary nucleus. They were minimally coded. They contacted 64 Purkinje cells. From these, the cerebellar nucleus obtained 64 maximally coded signals. These converged again in the frontal cortex to 8 maximally coded signals. There was a topological well-ordering in them due to the on-off gradient of the markers involved. This well-ordering allowed these axons to dock topologically correctly in the red nucleus again and, via further signal convergence, supply the original on-off signal pair with its input.

But let us imagine that the red nucleus was capable (in the course of evolution) of treating the eight signals arriving from the cortex, which originated from the eight climbing fibres, as independent inputs. Then these eight signals would do exactly what all the other signals from the cortex in the nucleus ruber would do. They would pull towards the motor targets, if present, but in addition to the side-changing nucleus, the nucleus olivaris. Before signal convergence, they would now form their own projection axons, which would pull from the nucleus ruber to the nucleus olivaris. There, they generate 8 input neurons, which in turn contact a sufficient number of " " interneurons, thus beginning a second stage of signal divergence. Each neighbouring pair of new input signals would belong to a new elementary matrix in the spinocerebellum, 7 in total.

Something similar could happen with the climbing fibre signals of the elementary matrix B, which would also undergo a new stage of signal divergence. This would give us 7 new offshoots of the elementary matrix B in the cerebellum. It would not be difficult to position these so that the 7 new elementary matrices derived from matrix A would each have a matching partner from the matrices derived from elementary matrix B. This would allow a more detailed angle analysis using the same principle.

Alternatively, it would be possible for the 8 output neurons formed in the olivary nucleus to project to the cerebellum, but then undergo a second stage of signal divergence within the olivary nucleus. This would cause the olivary nucleus to expand spatially.

Mathematically, this means that the first divergence level forms a steady superposition function according to the cable equation for an on-off signal pair, which provides the excitation of the climbing fibres at 8 support points. If each sub-interval is now divided again into 7 parts, the function values at 64 support points are obtained. The extreme value (minimum or maximum) remains unchanged, but the step size becomes extremely small.

What consequences would this have on the appearance of the spinocerebellum?

First, a kind of cylinder (primary cylinder) would be formed per segment, which would accommodate 64 Purkinje cells on each half, 8 rows with 8 columns on each half of the cylinder. This means two elementary matrices per segment.

This rather slender cylinder would now merge into another cylinder (secondary cylinder), which would have seven times the circumference because it would contain seven times the number of elementary matrices. The circumference must be divided by the number π to obtain the diameter. The new cylinder section would then have (approximately) 2.23 times the diameter. The spinocerebellum would more than double its diameter at this point.

A further stage of signal divergence would double the diameter of the next cerebellum cylinder.

At the same time, each individual elementary matrix would curve outwards slightly due to lack of space, forming a kind of arch or lobe. In the first cylinder section of the " ", we would have two such arches or lobes separated by furrows.

In the second cylinder section with the next higher level of divergence, we would already have seven such lobules or arches separated by furrows. In the cylinder section with the third level of signal divergence, the number of lobes and furrows would increase sevenfold again. This would create the typical cerebellum surface with its cortical sections bulging between two furrows, known as foliate (Latin for leaf).

With increasing levels of signal divergence, the angular resolution would become significantly more accurate, but this process is limited by the number of Purkinje cells available. This is especially true since the spinocerebellum uses only about one-third of the Purkinje cells, with the rest performing their work in the pontocerebellum.

It has not been mentioned that, at a certain stage of evolution, the climbing fibres in the cerebellum – and probably also in the spinocerebellum – contact not only the Purkinje cells but all accessible interneurons. The climbing fibres excite, possibly only slightly, the stellate cells, the basket cells and the Golgi cells. They may transmit the current on-off marker of the climbing fibre via these synaptic contacts so that the interneurons informed in this way know which neurons carry the intrinsic signal of this climbing fibre and which carry the competing signals.

The function of the Lugaro cells and tufted cells in the cerebellum is not analysed in detail in this chapter. They apparently serve the life support system and link its output to the cerebellar input.

In the next chapter, we will look at the circuitry and signal processing of the pontocerebellum. One thing in advance: the circuitry is the same. But the input is different. The recursion of the elementary matrices results in recursion in the pontocerebellum, which, however, is interpreted as a layering of a neural network.